Two’s complement: what is it and how to calculate it?

In mathematics, the 2s complement is a technique used in computers to represent the integers. It is a well-known operation for representing negative numbers in coding language. The binary variables 0 and 1 are used in this technique.

The 1s and 2s complements are frequently used in computers for the representation of positive and negative numbers. 1s complement is not capable of representing negative numbers. In this article, we are going to describe the two’s complement with its definition, conversions, and examples.

What is the two’s complement?

The technique used to encode the positive and negative numbers in the form of binary numbers 0 & 1 is said to be the two’s (2s) complement. The computer languages and logical gates (AND, OR, XOR, NAND, NOT) are widely used binary variables to encode and decode.

 The two’s complement is specially invented for the conversion of negative numbers in the form of binary variables. As 1s complement is only capable to convert the positive numbers into machine language.

The radix complement used twos complement as a perfect example. The 1s complement can be determined easily by inverting the binary number or binary numbers of decimals such as converting all the 0s into 1s and all the 1s into 0s.

While the 2s complement can be determined by adding 1 to the least significant bit of the 1s complement or inverted binary number. Now we are going to describe the conversion of binary and decimal numbers into twos complement.

Conversions

Here we will discuss how to convert the binary number, positive decimal number, and negative binary number into two’s complements.

Binary to 2s complement

Here are the steps to convert the binary numbers into twos complement.

1. Take the binary number either positive or negative.
2. After that take the transpose of the given binary number such as inverting the 0s into 1s and vice versa. This inversion of the variables of the binary numbers is known as the one’s complement.
3. Add one to the least significant bit after the inversion of the binary variables.
4. The final result after adding 1 to the LSB is the two’s complement.

By following the above steps, you can easily convert the binary variables into twos complement. Here are a few examples to learn how to convert binary variables into twos complement. 

Example 1

Convert the binary variable 1110001100101 into 2s complement. 

Solution

Step 1: First of all, write the given binary number and invert all the variables such as 0s to 1s and 1s to 0s.

Binary number = 1110001100101

Transpose of 1110001100101 = 0001110011010

Step 2: Now add 1 to the least significant bit of the transpose of 1110001100101 to get the two’s complement result.

Step 3: Write the result of the two’s complement.

The two’s complement of 1110001100101 = 0001110011011

A 2s complement calculator can be used to solve the above problem to avoid calculations

Example 2

Convert the binary variable 101010101010 into 2s complement. 

Solution

Step 1: First of all, write the given binary number and invert all the variables such as 0s to 1s and 1s to 0s.

Binary number = 101010101010

Transpose of 101010101010 = 010101010101

Step 2: Now add 1 to the least significant bit of the transpose of 101010101010 to get the two’s complement result.

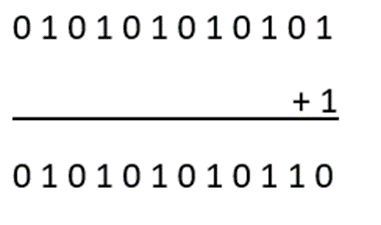
Step 3: Write the result of the 2’s complement.

The 2’s complement of 101010101010 = 010101010110

Decimal to twos complement

Here are the steps to convert the positive and negative decimal numbers into twos complement.

For a positive decimal number

To convert the positive decimal number into twos complement, follow the below steps.

1. Take a positive decimal number and convert it into a binary number.
2. After that take the transpose of the given binary number such as inverting the 0s into 1s and vice versa. This inversion of the variables of the binary numbers is known as the one’s complement.
3. Add one to the least significant bit after the inversion of the binary variables.
4. The final result after adding 1 to the LSB is the 2’s complement of a positive binary number.

For a negative decimal number

To convert the negative decimal number into twos complement, follow the below steps.

1. Take a negative decimal number and convert it into a binary number with respect to a positive number (without a negative sign).
2. After that calculate the two’s complement of the binary number with the help of the above steps.
3. After that take the transpose of the 2’s complement of positive numbers such as inverting the 0s into 1s and vice versa.
4. Add one to the least significant bit after the inversion of the binary variables.
5. The final result after adding 1 to the LSB is the 2s complement of a negative binary number.

By following the above steps, you can easily convert the positive and negative decimal numbers into twos complement. Here are a few examples to learn how to convert the positive & negative decimal into twos complement. 

Example I: For a positive decimal number

Convert the positive decimal number 597 into two’s complement.

Solution

Step 1: First of all, write the given positive decimal number and convert it into a binary number system.

positive decimal number = 597

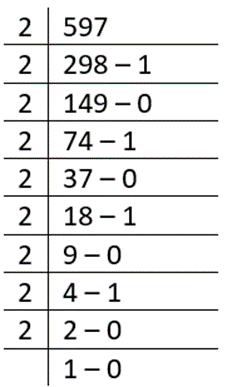
The binary number of 597 = 1001010101

Step 2: Invert all the variables of the calculated binary number 1001010101 such as 0s to 1s and 1s to 0s.

Binary number = 1001010101

Transpose of 1001010101 = 010101010101

Step 3: Now add 1 to the least significant bit of the transpose of 101010101010 to get the two’s complement result.

Step 4: Write the result of the 2s complement.

The 2’s complement of 1001010101 = 010101010110

Example II: For a negative decimal number

Convert the negative decimal number -677 into two’s complement.

Solution

Step 1: First of all, write the given negative decimal number and convert it into a binary number system with respect to the positive number.

Negative binary number = -677

The binary number of 677 = 1011100101

Step 2: Invert all the variables of the calculated binary number 1011100101 such as 0s to 1s and 1s to 0s.

Binary number = 1011100101

Transpose of 1011100101 = 0100011010

Step 3: Now add 1 to the least significant bit of the transpose of 1011100101 to get the two’s complement result.

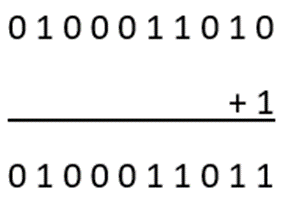
The 2s complement of 677 is 010011011

Step 4: Now take the two’s complement of the positive number and treat it as the binary variable and repeat the steps of converting the binary into twos complement.

The transpose of 010011011 = 101100100

Step 5: Now add 1 to the least significant bit of the transpose of 010011011 to get the two’s complement result.

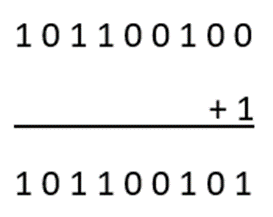
Hence,

The two’s complement of -677 = 101100101

Final words

The two’s complement is discussed with conversion and definition in this post. Now you are able to convert the binary number system or decimal number system into 2s complement easily just by following the above-mentioned steps.